Knotting semimetals in topological electrical circuits
SUTD – Amanda Sutrisno, Yee Sin Ang and Lay Kee Ang
NUS – Ching Hua Lee
University of Wurzburg - Tobias Hofmann, Tobias Helbig, Martin Greiter & Ronny Thomale
University of Chicago - Yuhan Liu
Sun Yat-sen University - Yuhan Liu and Xiao Zhang
Scientists created exotic states of matter using electrical circuit enhanced by machine-learning algorithm
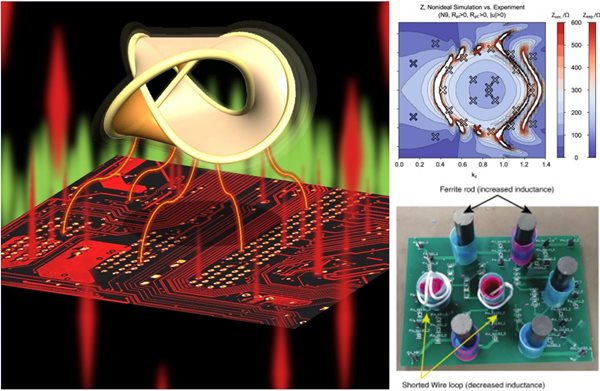Imaging nodal knots in momentum space through topolectrical circuits.
Invented more than 15,000 years ago, knots represent one of the earliest technological breakthroughs at the dawn of human history that kick-started the subsequent rise of human civilisation. Even today, we are still relying on knots in our daily life. Shoelace knots, for instance, have played a critical role in keeping shoes firmly on our feet for generations. Although knots are ancient inventions, the scientific and mathematical significance of knots were only discovered about 200 years ago.
Famed mathematicians, such as Carl Frederich Gauss and Peter Guthrie Tait, developed the general recipes for constructing different knots, and the mathematical rules that govern the classifications of knots according to their mathematical behaviours. Today, knot theory has formed one of the central pillars in many areas, including computer science, molecular biology, protein folding, DNA engineering, and drug discovery.
Intriguingly, the electronic properties of a peculiar type of metals, known as the nodal knot semimetals, can also exhibit complex behaviours that mathematically mimic knots. These peculiar knots are known as the momentum space knot, which arises when several electronic bands are intertwined and entangled together. Simply put, the concept of electronic bands provides a powerful physics picture which is particularly useful for describing the electronic properties of solids. Momentum space is the "landscape" that hosts such electronic bands.
For instance, electrically insulated solids typically have pockets of bands that are well-separated by empty voids - these empty voids in momentum space serve as a “no-man zone” that forbids electricity flow, thus rendering such material an electrically insulating property. On the other hand, the relatively large abundance of electronic bands and the absence of voids in metals allow electricity to flow through it more effortlessly making them good conductors.
What makes nodal knot semimetals especially unusual when compared to normal metals is that the electronic bands intertwine and entangle to form knotted structures in momentum space. This is mathematically equivalent to the knots we encounter in everyday life.
Although nodal knot metals have been predicted to exist in several crystals, synthesising these exotic crystals and probing the subtle momentum space knots remains a formidable task. To remedy such difficulties, physicists from Singapore and Germany have come up with a new class of designer electrical system in 2018, which is based entirely on an electrical circuit board. Such designer electrical circuit, dubbed topolectrical circuits, can emulate the complex physical behaviour of crystalline solid materials using ubiquitous electrical components such as resistors, capacitors, inductors and operational amplifiers. Leveraging on their enormous design flexibility, topolectrical circuits have been widely used to illustrate exotic physics phenomena in recent years.
Reporting in Nature Communications, physicists from Singapore (National University of Singapore and Singapore University of Technology and Design), Germany (University of Würzburg) and China (Sun Yat-sen University) have achieved a breakthrough in the synthesis and the measurement of momentum space nodal knots using topolectrical circuits.
"The research community has come a long way in the discovery of exotic phases of matter. More than a decade ago, the first topological insulator was synthesised, marking the first time robust topologically protected phenomena was detected in a real material. Today, we have not only engineered a sophisticated topological system based on knotted structures, but also realised it with low-cost, ubiquitous electrical components" said Dr Ching Hua Lee, Assistant Professor of National University of Singapore, who led the international research team, and pioneered the approach of using topolectrical circuits to study fundamental physics phenomena.
A rather unusual aspect of the momentum space knots is the existence of a smoking gun electrical signature at the boundary of the nodal knot metal, commonly known as the "drumhead states". Measuring drumhead states in solid materials is however highly challenging, and typically requires state-of-the-art instruments, such as high energy synchrotron X-rays and ultrahigh vacuum environments.
In contrast, probing drumhead states in topolectrical circuits requires only simple electrical measurements which can be readily carried out in most labs.
"Topological effects require very precise values of inductor/capacitor components. To counteract this difficulty, we used machine learning to find variations of the circuit design which displayed the same topological phenomena but can be constructed using less precisely made parts," said Amanda Sustrino, a research team member from the Singapore University of Technology and Design.
Aided by machine learning algorithms, the team has designed topolectrical circuits operating at “sweet spots” that are particularly robust against electrical noise. This novel design allows the elusive electrical signatures of drumhead states to be unambiguously identified.
"The ability to control electrical circuit using topology may offer a new route towards electrical signal processing, remote sensing, and digital information processing using inexpensive and low power components. These aspects could be tremendously important for future technologies such as IoT and beyond 5G networks," said Assistant Professor Yee Sin Ang from the Singapore University of Technology and Design.
Reference:
Imaging nodal knots in momentum space through topolectrical circuits, Nature Communications (DOI: 10.1038/s41467-020-17716-1)
Acknowledgements:
The work in Würzburg is funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) through Project-ID 258499086 - SFB 1170 and through the Würzburg-Dresden Cluster of Excellence on Complexity and Topology in Quantum Matter – ct.qmat Project-ID 39085490 - EXC 2147. T. Helbig was supported by a Ph.D. scholarship of the Studienstiftung des deutschen Volkes, Germany. X.Z. is supported by the National Natural Science Foundation of China (Grant No. 11874431), the National Key R&D Program of China (Grant No. 2018YFA0306800), and the Guangdong Science and Technology Innovation Youth Talent Program (Grant No. 2016TQ03X688). A.S., Y.S.A., and L.K.A. are supported by A*STAR-IRG (A1783c0011) and Singapore Ministry of Education (MOE) Academic Research Fund (AcRF) Tier 2 grant (2018-T2-1-007). Open access funding provided by Projekt DEAL.